Moebiustransformationen: Weitere einfache Beispiele mit Werten aus Indra's Pearls

Beispiel 7:
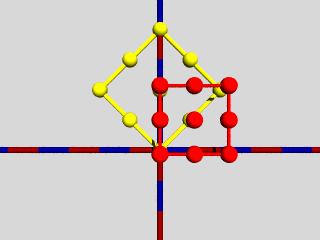
Die Möbiustransformation T(Z)=az entspricht der Multiplikation zweier komplexer Zahleh, man erhält also eine Drehstreckung, die hier an einem kleinen Gitter demonstriert wird, dabei sind die Originalpunkte für die bessere Sichtbarkeit um eine Einheit nach vorn geschoben.

Multiplikation mit 1+i: (Wird im Buch S. 41 vorgestellt)

a = 1 + 1*i
b = 0 + 0*i (beliebig)
c = 0 + 0*i
d = 1 + 0*i



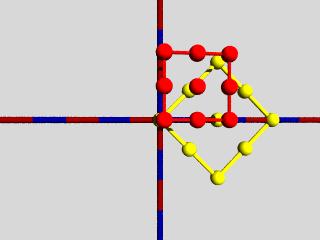
Sehen wir uns dieses Beispiel auch für a=1-i an: Der Streckfaktor bleibt erhalten, da sich der Betrag(a) nicht ändert, die Drehung geht in der entgegengesetzte Richtung:



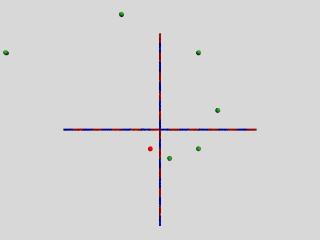
Multiplikationen mit a = 1 + i und mit a = 1 - i können auch mehrmals auf einen Startwert z angewendet werden. Man erhält dann Spiralen, die sich gegen bzw. im Uhzeigersinn drehen. Dies führt uns zum Kapitel iterierte Abbildungen.





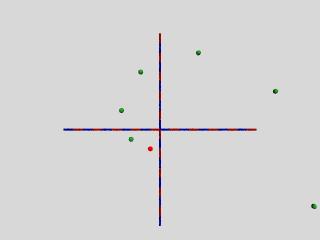
Vor Beginn des nächsten Kapitels noch einige Bemerkungen zur iterierten Drehstreckung:

Im folgenden Applet ist der Betrag von a = 1 (wenigstens beinah ist's mir gelungen, a auf den Einheitskreis zu legen), sowohl a als auch der Startwert z sind mit gedrückter Maustaste veränderbar.

Man erkennt: Für die Drehstreckung az (a,z komplex) ist 0+0i immer - unabhängig von a und z - Fixpunkt, denn T(O)=O.
Unabhängig von z gilt:

1. Ist der Betrag von a=1, dann erhält man konzentrische Kreise um den Fixpunkt
2. Ist der Betrag von a<1, dann erhält man Spiralen zum Fixpunkt hin, dieser wird dann anziehender Fixpunkt genannt
3. Ist der Betrag von a>1, dann erhält man Spiralen vom Fixpunkt weg, dieser wird dann abstoßender Fixpunkt genannt

An den interaktiven Beispielen (mit geogebra)im nächsten Kapitel erkennt man schnell, dass die Wahl der Anfangswerte schnell zu 'ungeordneten, unschönen' Bildern führen kann.

• Zum Seitenanfang