Moebiustransformationen
Komplexe Abbildungen
Auch in diesem Kapitel kann man auf dem interaktiven Lernpfad einige interaktive Applets ausprobieren.
Beispiel 1: Die Abbildung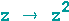 
, wobei z eine komplexe Zahl sein soll.
Bei der Wiederholung komplexer Zahlen (siehe Schaltfläche oben) wurde auch die Multiplikation komplexer Zahlen z1z2, die einer Drehstreckung entspricht, vorgestellt:
z2 wird gestreckt, Streckfaktor ist der Betrag von z1. Zusätzlich wird z2 noch um den Winkel gedreht, den z1 mit der x-Achse bildet.
Sehen wir uns mal an, was die Abbildung 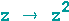mit den komplexen Zahlen im Gitter von
z1 = -5 -5i bis z2 = 5 + 5i macht. In der ff. Abbildung ist das Gitter in roter Farbe dargestellt, die Bilder in gelber Farbe.
Bei Mausklick aufs Bild wird das zugehörige pov-Skript gezeigt.
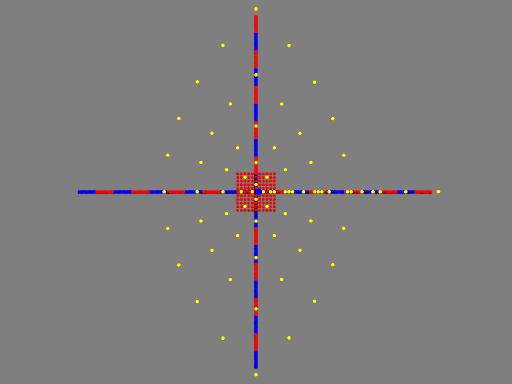
Lädt man sich das Skript runter, dann kann man durch Änderung der Schleifenzähler das Gitter einfach verschieben und erhält dann andere Abbildungen. Ausprobieren!
-
Bemerkung zur Programmierung in PoVRay:
Die Länge des Zeigers kann auch mit vlength(punkt) berechnet werden.
Der mit der arc cos -Relation berechnete Winkel ist im Bogenmaß, muss daher noch in Grad umgewandelt werden.
#macro quadratzahl (X,Y,Z, farbe)
#local punkt =<X,Y,Z>;
#local LP= sqrt(X*X+Y*Y+Z*Z);
#local winkel=acos(X/LP);
#local drehung=winkel*180/pi;
#local bild=sphere {punkt*LP, 0.5 pigment{farbe} rotate <0,0,drehung> }
bild
#end
Der Aufruf des Makros wird dann einfach in die verschachtelte Zählschleife fürs Gitter eingebunden.
Zur Wiederholung, wer's denn braucht:
Bogenmaß und Skalarprodukt:
Beispiel 2: Eine Exponentialfunktion muss her: e z.
Sehen wir uns an, was bei dieser Abbildung mit einer Geraden geschieht:
Die Punkte A und B, die die Gerade festlegen, können mit gedrückter Maustaste bewegt werden.
Zieht man dann P entlang der Geraden, dann durchläuft das Bild von P unter unserer Abbildung eine "Schnecke": Setze z. B B auf (-3/-2) und A auf (-2/6).
-
Mathematische Bemerkungen zur e-Funkton mit komplexen Exponenten:
Ersetzt man ex durch eix, so muss man sich fragen, was das überhaupt bedeuten soll.
Zur Antwort benutzen wir die Taylorreihenentwicklung von ex:
(Mit sog. Taylorreihen werden Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen angenähert )
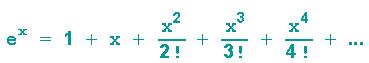
und ersetzen x durch ix:
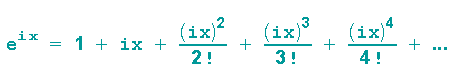
Wir setzen i2=-1 ein und spalten die Summe in einen Real- und einen Imaginärteil auf:
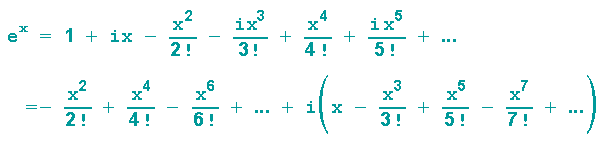
Als Real- um Imaginarteil erhalten wir interessanterweise genau die Taylorreihen von cos x und sin x !
Also:
eix = cos x + i sin x
Diese auf Leonhard Euler zuruckgehende Beziehung ist eine der wichtigsten mathematischen Formeln uberhaupt!
Sehen wir uns noch an, was sie für die Winkel 360° und 180° liefert:
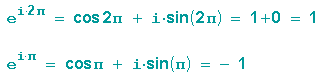
... und wählt man die Exponentialdarstellung für komplexe Zahlen, dann liefern uns die Potenzgesetze freundlicherweise auch gleich die Regel für die Multiplikation komplexer Zahlen in der Darstellung mit Polarkoordinaten:
| © 2011 Asti | Links für Unterricht | PoVRay-Site | Mathematische Streiflichter | Algorithmische Kunst | Webdesign |