Freiheitsgrade einer Möbiustransformation
Ändert man Bestandteile eines Systems, so erhält man dennoch manchmal das selbe Ergebnis.
Der Begriff Freiheitsgrad legt fest, wieviel solcher Systembestandteile man ändern kann und dabei immer noch das selbe Ergebnis erhält.
Hat man beispielsweise eine Messung aus 5 Messwerten und berechnet daraus das arithmetische Mittel, so kann man 4 Einzelwerte beliebig ändern - der 5. Wert ist dann festgelegt - und immer noch das selbe arithmetische Mittel erhalten.
Man sagt also: Eine Mittelwertsberechnung aus 5 Einzelwerten hat 4 Freiheitsgrade (es sind 4 Parameter unserer Rechnung frei wählbar)..
Ein kleines bisschen allgemeiner formuliert: Ein System kann sich gegenüber einer bestimmten Anzahl von Größen als unabhängig erweisen. Diese (An)zahl entspricht dann der (An)zahl der Freiheitsgrade.
Sehen wir uns die Anzahl der reellen Freiheitsgrade der Möbiustransformation an:
Spontane Antwort: Es gibt wg. der 4 komplexen Zahlen a,b,c und d, die ja jede für sich 2 Freiheitsgrade hat, da sie aus 2 reellen Zahlen (hier: Anzahl von frei wählbaren Elementen) und i zusammen gesetzt ist, 8 reelle Freiheitsgrade. Und schon FALSCH geantwortet.
Also schauen wir mal genauer hin:
Wir ersetzten a,b,c und d durch ein Vielfaches, das k-fache (k ungleich 0):
a wird zu ka, b wird zu kb, c wird zu kc und d wird zu kd. Und wenn wir nun k so wählen, dass der 4. Parameter d zu 1 wird, dann bleiben nur noch 6 Freiheitsgrade übrig.
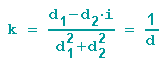
k kann dann wieder ausgeklammert und gekürzt werden.
Die 6 reellen Freiheitsgrade entsprechen drei komplexen Zahlen, die man als Punkte der komplexen Ebene betrachten kann und die die Möbiustransformation festlegen. Drei Punkte legen einen Kreis fest und somit kann man im nächsten Applet (Parameter a bis d sind fixiert, die Punkte R, S und T sind mit gedrückter Maustaste verschiebbar) ein bisschen mit Kreisen experimentieren:
|
|
Auch ineinander geschachtelte Kreise sind denkbar. Im ff. Applet ist b veränderbar:
|
|
| © 2011-2024 Asti | PoVRay-Site | Mathematische Streiflichter | Algorithmische Kunst | Webdesign |