Ein bisschen Theorie und Mathematik muss sein

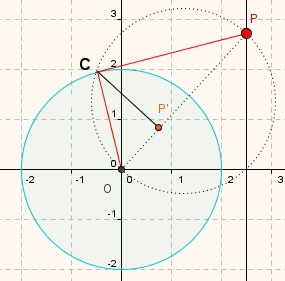
Wir haben den Bildpunkt P' bei der Inversion am Kreis als Lotfußpunkt im Thaleskreis festgelegt:



Auch die folgende Festlegung findet man:

P' ist der Bildpunkt von P bei einer Kreisspiegelung, wenn gilt:

  1. P und P' liegen auf derselben Halbgeraden durch den Mittelpunkt M des Inversionskreises.
  2. Für das Produkt ihrer Abstände von M gilt

Betrachten wir das (rechtwinklige) Dreieck OPC in obiger Abbildung (auf dessen Hypotenuse P und P' liegen) und wenden darauf den Kathetensatz an: Wir erhalten genau dieselbe Abbildungsvorschrift.

Wie finden wir nun eine Abbildungsvorschrift als anwendbare Formel?

Legen wir zunächst den Mittelpunkt M des Inversionskreises in den Koordinatenursprung und betrachten die Vektoren 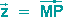und 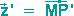als Zeiger komplexer Zahlen. Es gilt dann:

  1. (z')' = z (da die Kreisspiegelung involutorisch ist)

  2. mit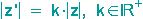

Sei nun die zu z konjugiert komplexe Zahl .

Nach der Abbildungsvorschrift (respektive nach dem Kathetensatz) gilt dann:



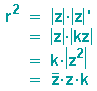
Wählt man als Inversionskreis nun den Einheitskreis (r=1 LE) mit M(0/0), dann folgt aus der letzten Zeile



Betrachtet man also die Abbildungsvorschrift

,

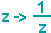dann wird durch sie jeder komplexen Zahl z der Gaußchen Zahlenebene eine zweite komplexe Zahl z' zugeordnet, die man durch Inversion am Einheitskreis mit nachfolgender Spiegelung an der reellen Zahlenachse erhält.



Formeln für Kreis und Gerade in kartesischen Koordinaten

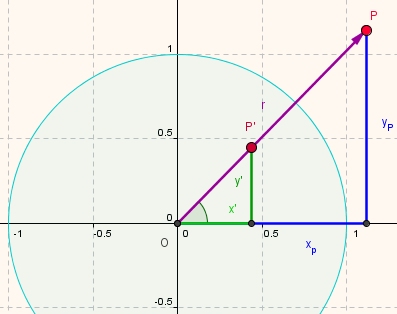
Ausgehend von Polarkoordinaten sind die kartesischen Koordinaten des Bildpunktes P' einfach herleitbar:

P habe den Abstand r vom Mittelpunkt des Einheitskreises (Inversionskreis), P' habe den Abstand r'. Die Winkel zur x-Achse seien und '.



Da P und P' auf ein und derselben Halbgeraden liegen, ist = '.

Für den Punkt P' gilt somit:



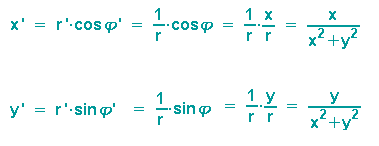
Wegen (P')'=P (die Kreisspiegelung ist ja involutorisch) gelten dieselben Formeln für x und y:



... und was fangen wir damit an? Na, wir werden hellseherisch und prophezeien, dass die Gerade y=-2x+1 auf den Kreis mit dem Mittelpunkt M(1/0,5) und dem Radius abgebildet wird:


... und umgekehrt muss dieser Kreis natürlich auch auf die Gerade y=-2x+1 abgebildet werden:


Wir haben richtige Voraussagen gemacht, die wir zum Abschluss unserer theoretischen Überlegungen noch rechnerisch überprüfen.

In die Geradengleichung

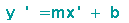
setzen wir die Formeln für die Abbildung ein,



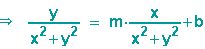
multiplzieren die Gleichung mit ihrem Nenner und bringen alle Terme auf eine Seite.



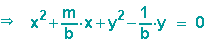
Mit Hilfe der quadratischen Ergänzung vervollständigen wir die Gleichung,



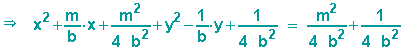
wenden die binomischen Formeln an und erhalten eine Kreisgleichung,



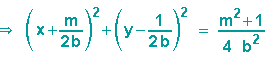
aus der wir Mittelpunkt und Kreisradius ablesen können.



Da wir ausschließlich Äquivalenzumformungen benutzt haben, können wir sagen: Zum Kreis mit Mittelpunkt M gehört die Gerade g, zur Gerade g gehört der Kreis mit Mittelpunkt M:




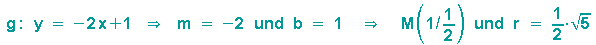
© 2009.2024 Asti PoVRay-Site