- Grundlagen
- Zusatzinfos zu Aufgaben
- Aufgaben 1 - 21
- Aufgaben 22 - 23
- Ebene in Normalenform
- Startseite Geometrie
- Startseite PoV-Theorie
- Startseite
Zunächst ein bisschen Theorie zur Normalenform der Ebene:
Die Normalenform der Gleichung einer Ebene - Theorie
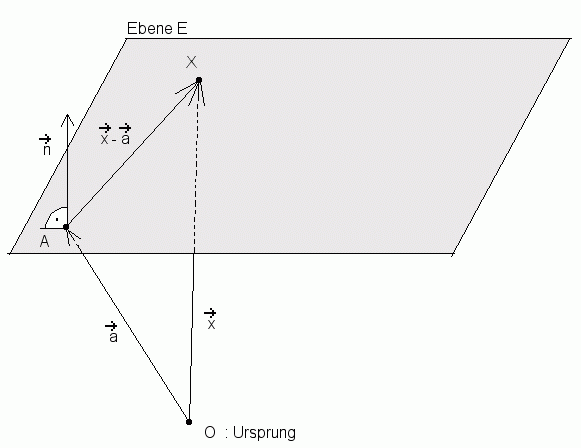
Auf einer Ebene E im 3-dimensionalen Raum liege ein Punkt A (x a / y a / z a), außerdem der "laufende" Punkt X (x/y/z).
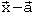 .
Der Normalenvektor (Lotvektor)
.
Der Normalenvektor (Lotvektor) 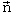 steht senkrecht auf
steht senkrecht auf 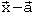 und auf allen anderen Vektoren der Ebene, d.h. das Skalarprodukt
und auf allen anderen Vektoren der Ebene, d.h. das Skalarprodukt 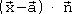 muss Null sein, da cos90°=0.
muss Null sein, da cos90°=0. Die Gleichung
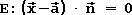 beschreibt also die Ebene E und wird Normalenform der Ebenengleichung genannt.
beschreibt also die Ebene E und wird Normalenform der Ebenengleichung genannt. Wird statt
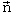 der Normaleneinheitsvektor
der Normaleneinheitsvektor 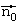 benutzt, dann spricht man von der HESSE'schen Normalenform der
Ebenengleichung:
benutzt, dann spricht man von der HESSE'schen Normalenform der
Ebenengleichung: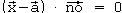 .
.
Info SKALARPRODUKT:
Das Skalarprodukt ist eine Verknüfung zweier Vektoren, für die das
Kommutativ- und das Distributivgesetz gelten soll und die eine Zahl
(kein Vektor!) zum Ergebnis hat.
Es ist wie folgt definiert:
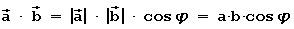
Vektoren sind als Vielfache der Einheitsvektoren in Richtung der 3
Koordinatenachsen darstellbar.
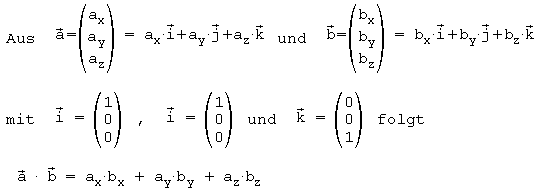
Die letzte Zeile liefert also die Rechenregel "Man bildet das
Skalarprodukt zweier Vektoren, indem man ihre Komponenten paarweise
miteinander multipliziert und die Produkte addiert".
Info HESSE'SCHE Normalenform und Abstandsbestimmung
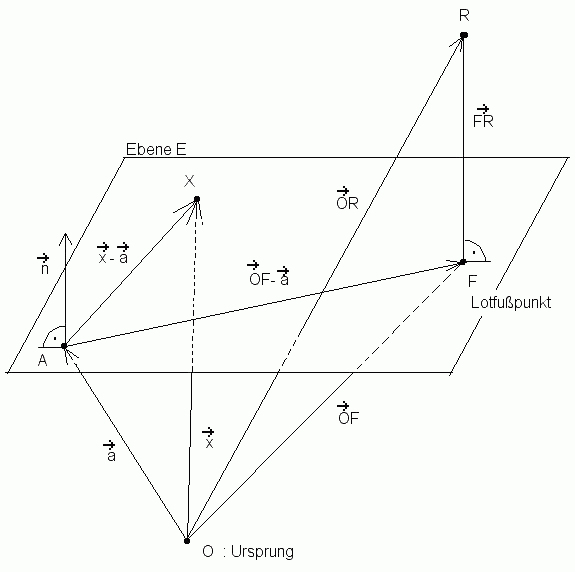
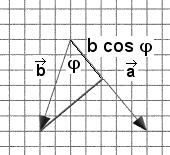
Betrachtet man einen Punkt R außerhalb der Ebene E, dann gibt der zu E
senkrecht Vektor FR den Abstand des Punktes R zu E an.
Es gelten die in der Abbildung dargestellten Beziehungen zwischen den
Vektoren.
Der Abstand des Punktes R von der Ebene E kann dann als Vielfaches vom
Normaleneinheitsvektor angegeben werden, also
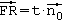
und
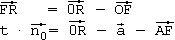 .
.
Da wir uns für t interessieren, multiplizieren wir die letzte Gleichung
mit 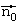 und erhalten
und erhalten

An dieser Stelle erkennen wir, dass man bei Einsetzen von (0/0/0) für
den Punkt R den Abstand der Ebene vom Ursprung mit 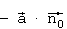 berechnen kann, dem
negativen Skalarprodukt aus dem Stützvektor und dem
Normaleneinheitsvektor.
berechnen kann, dem
negativen Skalarprodukt aus dem Stützvektor und dem
Normaleneinheitsvektor.
Die Normalenform der Gleichung einer Ebene - so geht's mit PoVRay
- Das Ziel :
- Die "Werkzeuge"
- Als erstes kommen die Transformationen für die dem Makro übergebenen Variablen für den Normalenvektor und den Stützvektor <xa, ya, za> , die du aus dem vorherigen Kapitel kennst. Die Normalenform der Ebene soll im rechtshändigen Koordinatensystem programmiert werden.
-
Als räumliche Darstellung der Ebene kann man eine Schnittmenge einer
Kugel mit der Ebene wählen, was den Vorteil hat, dass der Betrachter
sich die Ebene auch bei ungünstiger Lage noch vorstellen kann.
intersection{ plane {<xn, yn, zn> ,-Abstand pigment {Med_Purple transmit 0.8}hollow } sphere {<0,0,0> 10 pigment {White transmit 0.9} hollow} }//end intersection
Die Syntax des Schlüsselwortes plane ist plane{Normalenvektor, Abstand zum Ursprung}, - Mit einer if-Abfrage (siehe Grundlagen) wird gewährleistet, dass die Schnittmenge nur gezeichnet wird, wenn der Abstand der Ebene zum Ursprung kleiner als 10 ist, ansonsten soll der Text "Abstand zum Ursprung >10" ausgegeben werden. Auch das Text-Objekt wurde im Grundlagen-Kapitel erklärt.
-
Um den Normaleneinheitsvektor zu erhalten, muss die Länge des
Normalenvektors bestimmt werden:
Laenge=vlength(<xn, yn, zn>)
Die Komponenten des Normalenvektors müssen dann durch die Länge geteilt werden:
#local xno=xn/Laenge; #local yno=yn/Laenge; #local zno=zn/Laenge;
-
Für die Abstandsberechnung bietet PoVRay das Schlüsselwort vdot
zur Berechnung des Skalarproduktes:
#local Abstand= -vdot(<xn, yn, zn>/Laenge <xa, ya, za>);
-
Das Rückgängigmachen der Transformationen, um bereits fertiggestellte
Makros innerhalb des neuen Makro aufrufen zu können:
#local x_alt=-zn; #local y_alt=xn; #local z_alt=yn; #local xn=x_alt; #local yn=y_alt; #local zn=z_alt; #local x_alt=-za; #local y_alt=xa; #local z_alt=ya; #local xa=x_alt; #local ya=y_alt; #local za=z_alt; #local x_alt=-zno; #local y_alt=xno; #local z_alt=yno; #local xno=x_alt; #local yno=y_alt; #local zno=z_alt;
- Die Aufgabe: Programmiere nun das Makro EbeneN(xn,yn,zn, xa,ya,za) für die Darstellung einer Ebene in Normalenform im rechtshändigen Koordinatensystem und binde es in geometrei.inc ein. Kontrolliere es mit geeigneten Variablen.
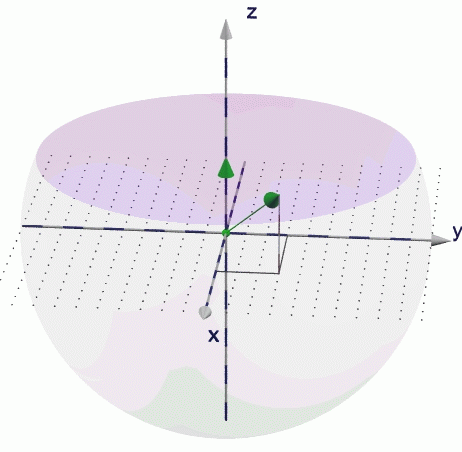
Im rechtshändigen Koordinatensystem soll mit
EbeneN_rechts(0,0,1,5,3,4)
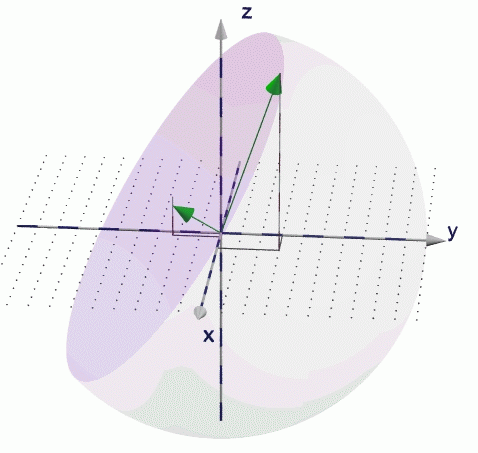
eine Ebene dargestellt werden, die auf der z-Achse senkrecht steht (ihr Normalenvektor ist also <0,0,1>). Sie soll den Punkt <5/3/4> enthalten. Dieser Punkt soll durch einen Vektor vom Ursprung aus dargestellt werden. Der Abstandsvektor soll ebenfalls dargestellt werden. Auch Ebenen, deren Normalenvektor "schief" ist, sollen auf die gleiche Art dargestellt werden. Im zweiten Bild wurde
EbeneN_rechts(1,-4.5,3,2,3,9)
dargestellt.
| © 2010 Asti | PoVRay-Site | Mathematische Streiflichter | Algorithmische Kunst |